Normal | Central Tendency

Not to be confused with Central Limit Theorem, is where the center or the middle location of the distribution is the average value of a probability distribution.

When given a collection of values, the Central Tendency is the tendency for values to settle in the middle of the value range. This observation is typical with data that may deviate from a given value by order of probability, meaning that the central tendency should be the desired value while those falling above or below are “deviated” from that desired value.

Note that the central tendency may not always be the desired value. For instance, in machining a product, the calibration of the machines may be off, meaning that the most common outcome is some way off the desired outcome, forcing the central tendency to be higher (or lower) than what is desired.

Finding a Central Tendency requires simple math; particularly “mean”, “median” or “mode” calculations.

Simple Explanation

Central Tendency gives the central value of the population or sample.

Calculator

Calculation

Mean or Average

Symbols

x (x-bar) means "average"

σ is "sigma" and means "standard deviation"

Σ is also called "sigma" (confusing) and means "sum"

x = ^{Σ x}⁄_n where n is number of values

Median

Place values in ascending or descending order and take the middle value. If two middle numbers (even total), then add two nums together and divide by two.

90, 98, 104, 104, 104
85, 90, 98, 104, 104, 104 = ^{(98 + 104)}⁄₂ = 101

Mode

The number occurring the most number of times.

85, 104, 90, 98, 104, 104

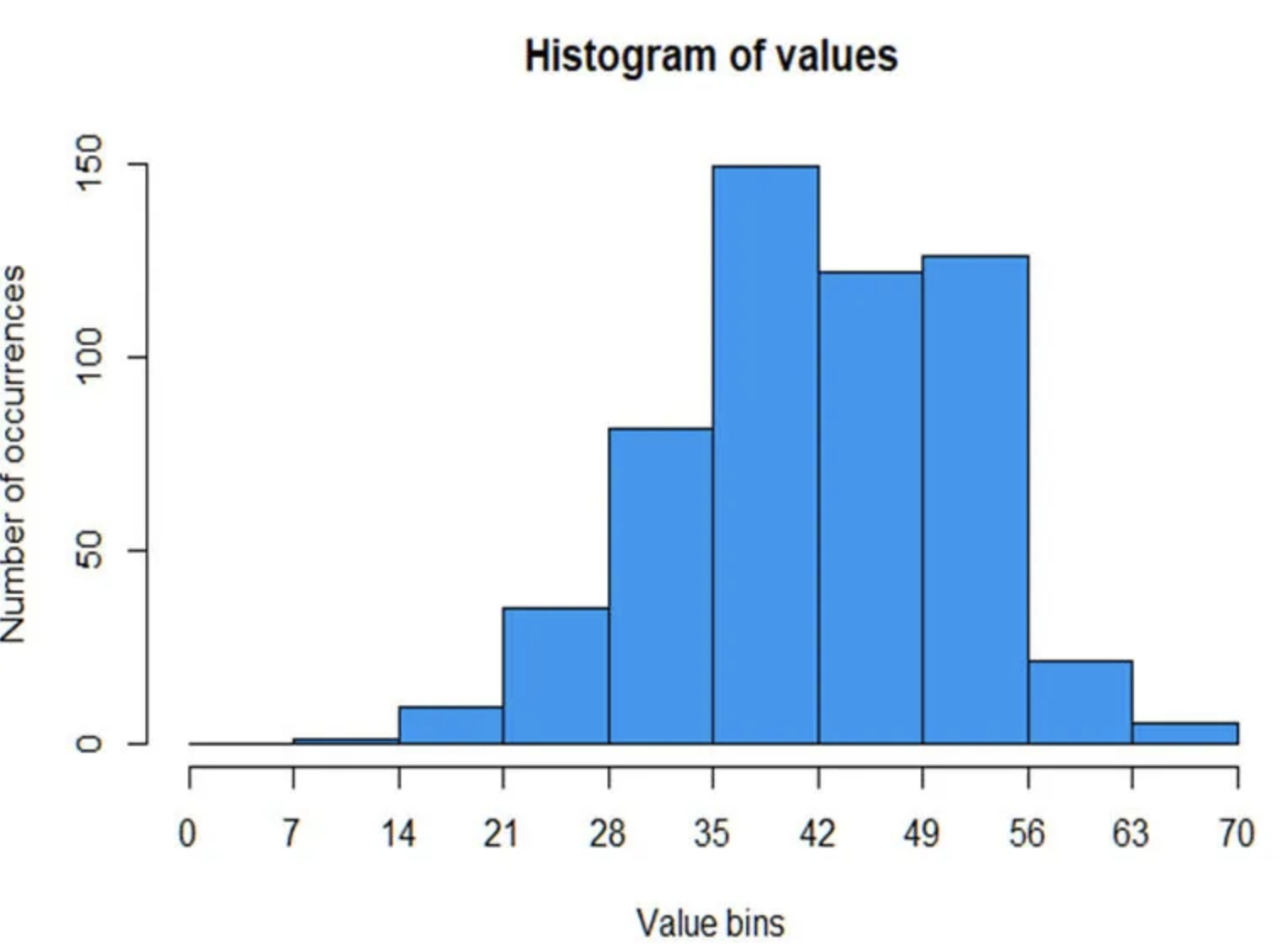
Mode in Histogram

In the below histogram, we can see that the highest peak is the mode, since
it represents the most common value.

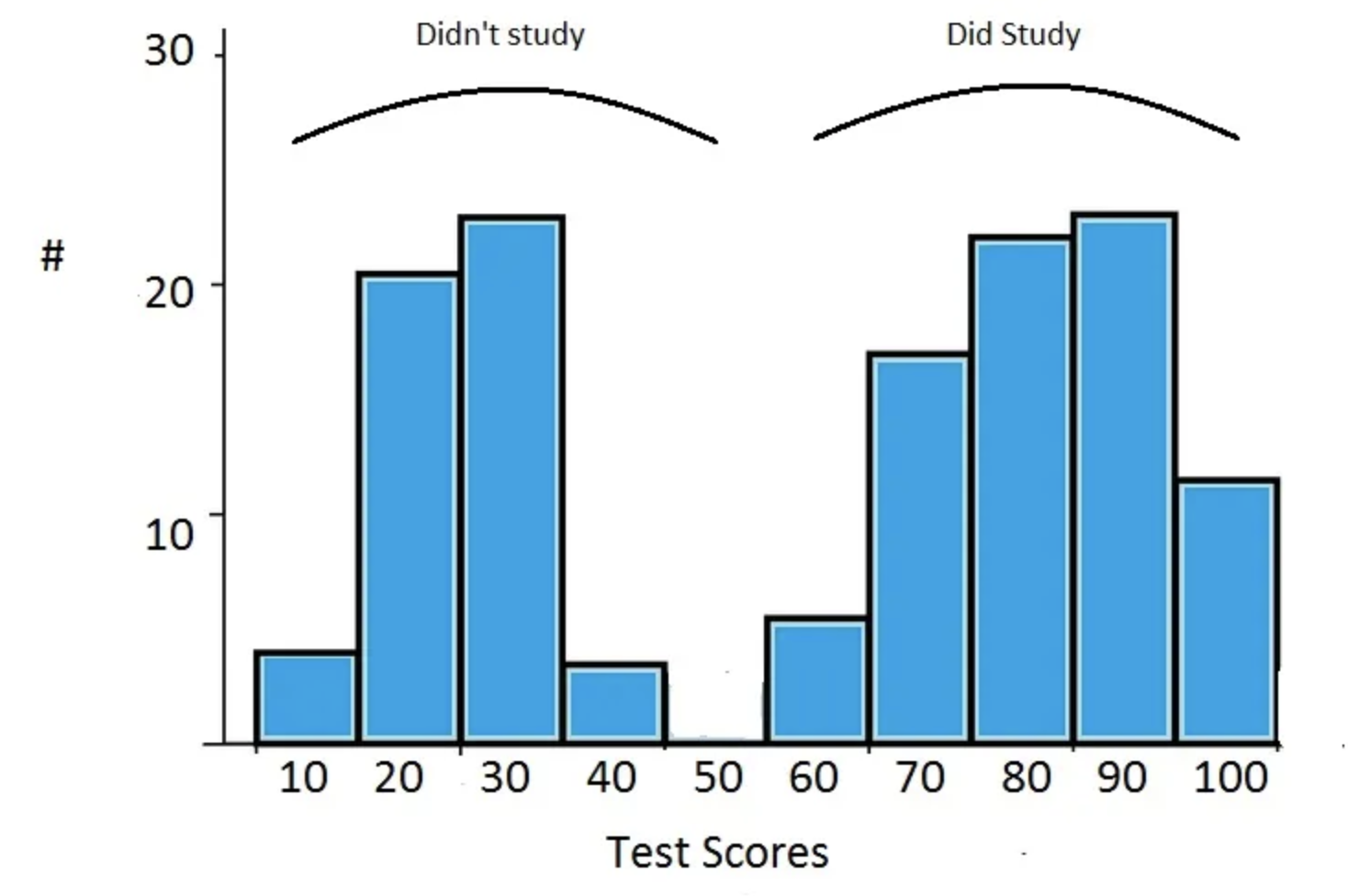
In a bi-modal histogram, we would say there are “two modes”. Hence
why it’s called bi-modal (two-modes).

← Back to Quality Management