DSP | Filters | IIR Filter
Calculators Theory Z-Domain Filters
Biquadratic PZ Placement Butterworth Chebyshev Prototypes IIR Filter
← Back to Digital Signal Processing
System Analysis 1
The following system;
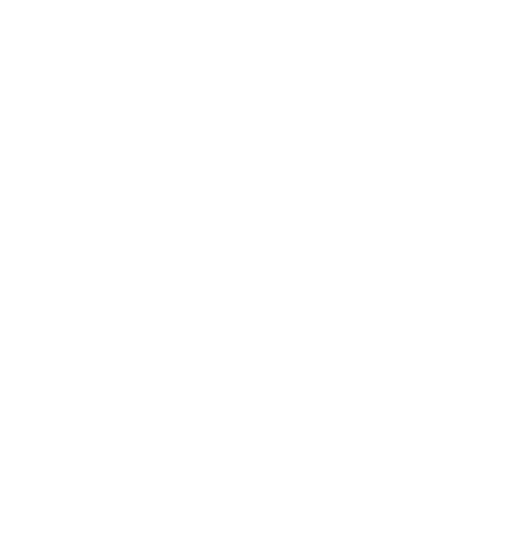
has the following transfer function;
\[G(z) = \frac{(z+0.54)(z+0.49)}{(z-0.12)(z-0.31)}\]Answer the following question giving answers to 4 decimal places.
If \(c_{2} = 0.31\) then determine \(d_{0}, d_{1}, d_{2}, c_{1}\);
\[\frac{G(z)}{z} = \frac{(z+0.54)(z+0.49)}{z(z-0.12)(z-0.31)} = \frac{A}{z} + \frac{B}{(z-0.12)} + \frac{C}{(z-0.31)}\]Cross-multiply and remove denominator;
\[G(z) = (z+0.54)(z+0.49) = A(z-0.12)(z-0.31)+Bz(z-0.31)+Cz(z-0.12)\]Determine \(A - z = 0\);
\[\displaylines{ = (0+0.54)(0+0.49) \\ = (0-0.12) + (B \times 0(0-0.31) = 0) + (C \times 0(0-0.12) = 0) \\ = 0.54 + 0.49 = A(-0.12)(-0.31) \\ \therefore A = \frac{0.54 \times 0.49}{-0.12 \times -0.31} \\ A = \frac{0.2646}{0.0372} = 7.1129 }\]MATLAB
z1 = 0.54; z2 = 0.49; p1 = -0.12; p2 = -0.31;
A = (z1 * z2)/(p1 * p2)
% ans =
% 7.1129
Determine \(B - z = 0.12\);
\[\displaylines{ = (0.12+0.54)(0.12+0.49) = B 0.12(0.12-0.31) \\ \therefore 0.66 \times 0.61 = B 0.12 \times -0.19 \\ B = \frac{0.66 \times 0.61}{0.12 \times -0.19} = -17.6579 }\]MATLAB
z1 = 0.54; z2 = 0.49; p1 = -0.12; p2 = -0.31;
B = ((p1 + z1) * (p1 + z2)) / (p1 * (p1 - p2))
% ans =
% -17.6579
Determine \(C - z = 0.31\);
\[\displaylines{ = (0.31+0.54)(0.31+0.49) = C 0.31(0.31-0.12) \\ \therefore 0.85 \times 0.80 = C 0.31 \times 0.19 \\ C = \frac{0.85 \times 0.80}{0.31 \times 0.19} = 11.5450 }\]MATLAB
z1 = 0.54; z2 = 0.49; p1 = -0.12; p2 = -0.31;
C = ((p2 + z1) * (p2 + z2)) / (p2 * (p2 - p1))
% ans =
% 11.5450
Decibels Per-Decade
For the real world reconstruction filter, it is designed to be an order 8 low pass analogue filter. It is desired to achieve -43dB of attenuation in the stop band. How many whole number of decades is the transition band likely to cover?
To answer this, recall that IIR filters attenuate at a rate of 20dB/decade per order;
\[\displaylines{ 8 * 20 = 160\text{dB/decade} \\ \therefore \text{the answer is: 1 decade} }\]System Analysis 2
A filter has the following realisation;
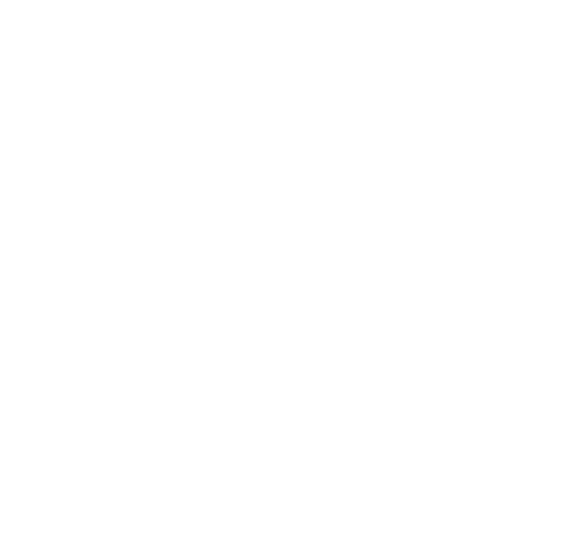
where the values of the multipliers are \(a_{1} = 0.35\), \(a_{2} = -0.72\), \(b_{1} = -0.32\) and \(b_{2} = 0.571\).
For the following transfer functions, determine the values of the coefficients;
\[\displaylines{ H_{1}(z) = \frac{z + \gamma_{1}}{z + \gamma_{2}} \\ H_{2}(z) = \frac{z + \gamma_{3}}{z + \gamma_{4}} }\]Looking at the inputs on the left and the outputs on the right, inverting the values for inputs, we have;
\[\displaylines{ \gamma_{1} = b_{1} = -0.32 \\ \gamma_{2} = a_{1} \times -1 = 0.35 \times -1 = -0.35 \\ \gamma_{3} = b_{2} = 0.571 \\ \gamma_{4} = a_{2} \times -1 = -0.72 \times -1 = 0.72 }\]Overall Transfer Function
For the overall transfer function;
\[H(z) = \frac{2z^{2} + z\beta_{1} + \beta_{2}}{z^{2} + z\beta_{3} + \beta_{4}}\]Determine the coefficients;
Since our transfer functions are parallel, we simply add them. Thus;
\[\displaylines{ H(z) = \frac{Y(z)}{X(z)} = \frac{z + \gamma_{1}}{z + \gamma_{2}} + \frac{z + \gamma_{3}}{z + \gamma_{4}} \\ \text{Thus, }\frac{z - 0.32}{z + 0.35} + \frac{z + 0.571}{z - 0.72} }\]Obtained the least common multiple, we place the LCM as the denominator of each fraction and in the numerator of each fraction we add the factors that we need to complete;
\[= \frac{(z - 0.32)(z - 0.72)}{(z + 0.35)(z - 0.72)} + \frac{(z + 0.571)(z + 0.35)}{(z - 0.72)(z + 0.35)}\]Multiplying out the numerators, gives us;
\[\displaylines{ z * z = z^{2} \\ z * -0.72 = -0.72z \\ -0.32 * z = -0.32z \\ -0.32 * -0.72 = 0.2304 }\]And;
\[\displaylines{ z * z = z^{2} \\ z * 0.35 = 0.35z \\ 0.571 * z = 0.571z \\ 0.571 * 0.35 = 0.19985 }\]Which results in;
\[= \frac{z^{2} - 0.72z - 0.32z + 0.2304}{(z + 0.35)(z - 0.72)} + \frac{z^{2} + 0.35z + 0.571z + 0.19985}{(z - 0.72)(z + 0.35)}\]Then, combine matched \(z\)’s;
\[= \frac{z^{2} - 1.04z + 0.2304}{(z + 0.35)(z - 0.72)} + \frac{z^{2} + 0.921z + 0.19985}{(z - 0.72)(z + 0.35)}\]Add the numerators, keeping the denominator as is;
\[\frac{2z^{2} - 0.1190z + 0.4303}{(z + 0.35)(z - 0.72)}\]Finally, multiply the values and combine in the denominator;
\[\displaylines{ z * z = z^{2} \\ z * 0.35 = 0.35z \\ -0.72 * z = -0.72z \\ 0.35 * -0.72 = -0.252 }\]Which results in;
\[\frac{2z^{2} - 0.1190z + 0.4303}{z^{2} - 0.37z - 0.252}\]Therefore;
\[\displaylines{ \beta_{1} = -0.1190 \\ \beta_{2} = 0.4303 \\ \beta_{3} = -0.37 \\ \beta_{4} = -0.252 \\ }\]MATLAB
z1 = -0.32; p1 = 0.35; z2 = 0.571; p2 = -0.72;
z1out = z1 + p2 + z2 + p1
% ans =
% -0.1190
z2out = z1 * p2 + z2 * p1
% ans =
% 0.4303
p1out = p1 + p2
% ans =
% -0.37
p2out = p1 * p2
% ans =
% -0.252
System Analysis 3
A filter has the following realisation;
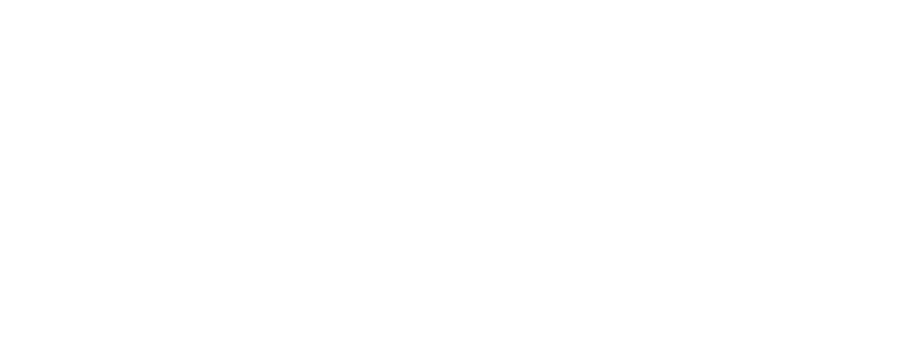
where the values of the multipliers are \(a_{1} = -0.37\), \(a_{2} = 0.54\), \(b_{1} = 0.85\) and \(b_{2} = -0.76\).
Answer the following, giving answers to four decimal places.
For the following transfer functions, determine the values of the coefficients;
\[\displaylines{ H_{1}(z) = \frac{z + \gamma_{1}}{z + \gamma_{2}} \\ H_{2}(z) = \frac{z + \gamma_{3}}{z + \gamma_{4}} }\]Looking at the inputs on the left and the outputs on the right, inverting the values for inputs, we have;
\[\displaylines{ \gamma_{1} = b_{1} = 0.85 \\ \gamma_{2} = a_{1} \times -1 = -0.37 \times -1 = 0.37 \\ \gamma_{3} = b_{2} = -0.76 \\ \gamma_{4} = a_{2} \times -1 = 0.54 \times -1 = -0.54 }\]Overall Transfer Function
For the overall transfer function;
\[H(z) = \frac{z^{2} + z\beta_{1} + \beta_{2}}{z^{2} + z\beta_{3} + \beta_{4}}\]Determine the coefficients;
Since our transfer functions are series, we multiply them. Thus;
\[\displaylines{ H(z) = \frac{Y(z)}{X(z)} = \frac{z + \gamma_{1}}{z + \gamma_{2}} \times \frac{z + \gamma_{3}}{z + \gamma_{4}} \\ \text{Thus, }\frac{z + 0.85}{z + 0.37} \times \frac{z - 0.76}{z - 0.54} }\]Multiplying both sides, we have;
\[\displaylines{ H(z) = \frac{z^{2} - 0.76z + 0.85z - 0.646}{z^{2} - 0.54z + 0.37z - 0.1998} \\ = \frac{z^{2} + 0.09z - 0.646}{z^{2} - 0.17z - 0.1998} }\]Therefore;
\[\displaylines{ \beta_{1} = 0.09 \\ \beta_{2} = -0.646 \\ \beta_{3} = -0.17 \\ \beta_{4} = -0.1998 \\ }\]MATLAB
z1 = 0.85; p1 = 0.37; z2 = -0.76; p2 = -0.54;
z1out = z1 + z2
% ans =
% 0.09
z2out = z1 * z2
% ans =
% -0.646
p1out = p1 + p2
% ans =
% -0.17
p2out = p1 * p2
% ans =
% -0.1998