DSP | Theory | Sampling Theorem
Calculators Theory Z-Domain Filters
Quantization & Sampling Theorem Math Linear Systems Convolution Fourier Transform
← Back to Digital Signal Processing
Sampling (Nyquist) Theorem
The sampling theorem, also known as the Nyquist Theorem, states that a continuous signal can be properly sampled if, and only if, it does not contain frequency components above half of the sampling rate.
fs ≥ 2fmax
As such, an audio signal containing voice at 4khz must be sampled at 8khz or higher.
Quantization
Quantization is the process of converting a continuous (analog) input signal into a discrete (digital) response signal. Thus, the original continuous signal is defined by the characteristics of the discrete digital output but could, in theory, be converted back to the continuous analog state, provided it was properly sampled.
The following image presents four different types of signals;
|
1. Aperiodic continuous 2. Periodic continuous 3. Aperiodic discrete 4. Periodic discrete |
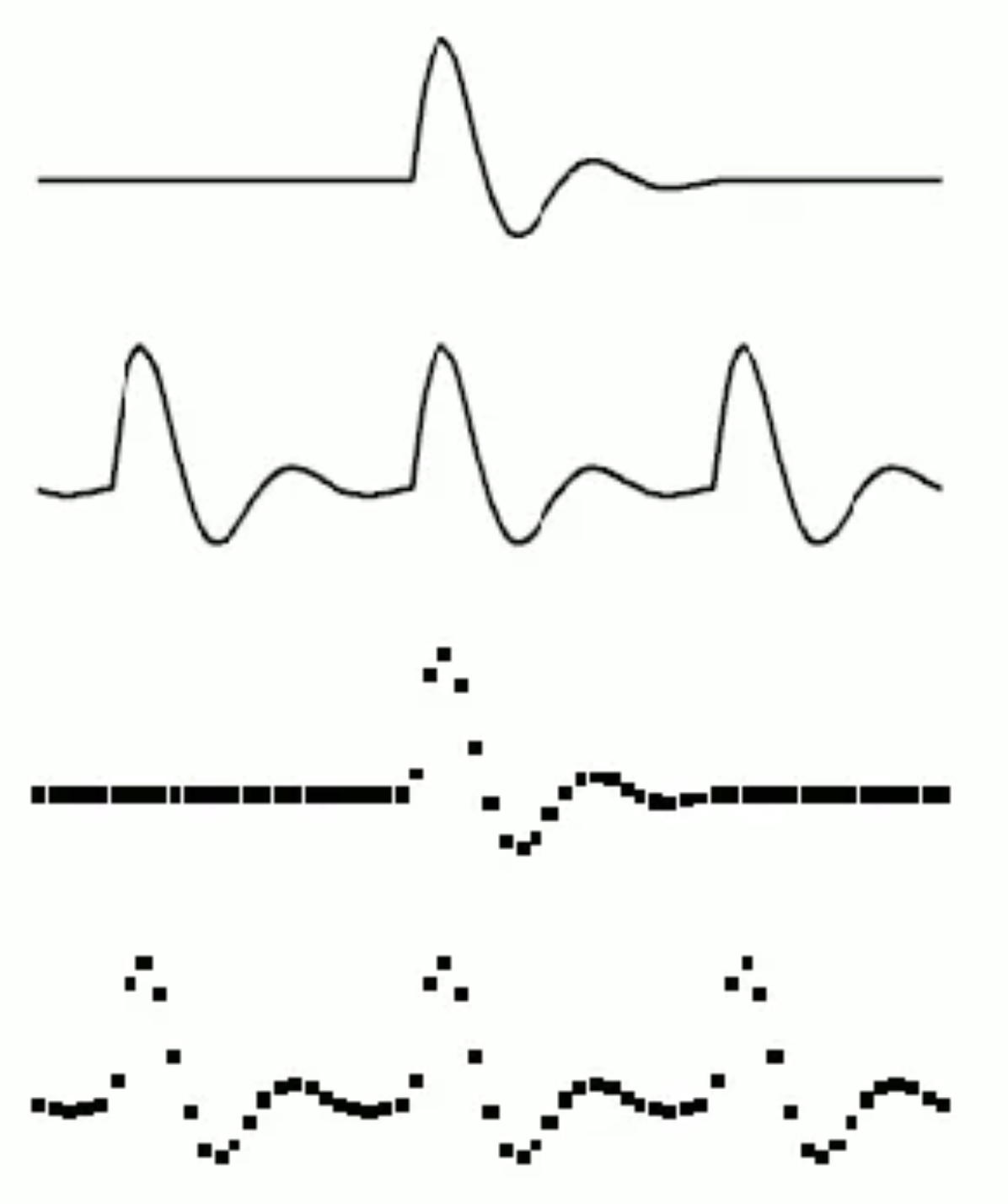
|
Antialiasing Filter
Before an analog signal enters an ADC (Analog-to-Digital-Converter), it is first passed through an analog filter. The analog filter removes frequency components above half of the sampling rate, resulting in a filtered analog signal. The analog filter is otherwise known as an antialias filter.
Without the antialias filter, the Sampling Theorem risks being violated. If this happens, then the signals entering the ADC can become indistinguishable from one another, resulting in an incorrect response signal.
For instance, if a signal contains 1khz and 20khz signals and the output signal is required to be 3khz maximum, then it would be necessary to filter out the 20khz signal, so that only the 1khz signal was converted to digital. Failure to do so results in undersampling which means the resolution of the quantization is insufficient to digitize the sample correctly, as in the image below.